[C032 zmol kg
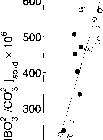
图3.3.25有孔虫方解石(O. univtrsa)氧同位素组成随[CO?-] (ECOo= const。~ 2032 //mol kg-1)。随着[CO3-]或pH值的增加,外壳在180度内耗尽。由Spero等人(1997)给出的壳ilaO与[CO?-]在暗区为-0.0022±0.0004'Xo (/nnol kg"1),在亮区为-0.0015±0.0008lXo (//mol kg-1)-1。
有孔方解石和S中<*>180对[CO2-]的观测和计算斜率的一致性,以及在合成碳酸盐中观察到的氧同位素效应之间的一致性(Kim和O'Neil。1997)和理论预测(第3.3.8节)。
与O. universa的培养资料比较
无机沉淀的氧同位素分配结果(C.9节)可与活有孔虫培养实验中观察到的shell¿180与[CO3-]进行比较(Spero等人,1997年)。为作比较,分数之间的和碳酸盐物种(5)和水必须只与[CO2-]而不是pH相对应,以便(a)避免与代谢效应相关的并发症,如共生藻类在光照下的光合作用,以及(b)确保培养基的SC02的pH值
®t• |
1 1 |
1 |
F ^ 0) |
(电视,电视,电视 |
1 |
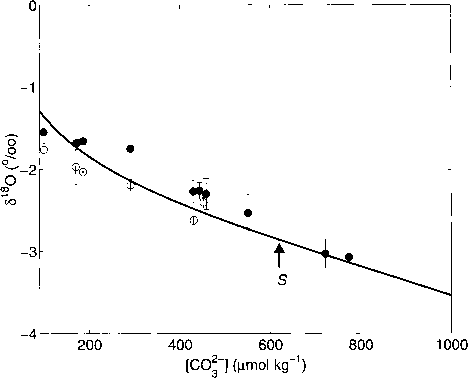
图3.3.26:有孔虫方解石氧同位素组成(闭圈/开圈:暗圈/高光圈)和理论预测的5 = [H2C03] + [HCO~] + [CO*-] vs. [CO*-](实线)。Spero等人(1997)给出的shell¿lsO vs. [CO*-]在恒定ECO2实验中的平均斜率为- 0.0022±(/¿mol kg-1)-1。理论预测的平均斜率为-0.0024±(/imol kg-1)-1。
图3.3.26:有孔虫方解石氧同位素组成(闭圈/开圈:暗圈/高光圈)和理论预测的5 = [H2C03] + [HCO~] + [CO*-] vs. [CO*-](实线)。Spero等人(1997)给出的shell¿lsO vs. [CO*-]在恒定ECO2实验中的平均斜率为- 0.0022±(/¿mol kg-1)-1。理论预测的平均斜率为-0.0024±(/imol kg-1)-1。
保持恒定,Spero等人(1997)的黑暗实验(SC02 = const。选择~ 2032 /zmol kg-1)进行比较。的分离的因素Usdowski et al.(1991)的报告提到了a淡水系统在19°C;在他们的实验中没有检验这种对温度的依赖性。另一方面,有孔虫在22°C的海水中培养。因为这两个系统不同的温度溶液中碳酸盐和方解石的盐度、绝对值(<5180)没有进行比较。然而,溶液(S)中主要碳酸盐组分与水之间分馏的计算斜率可以与有孔虫¿180的斜率作为[CO§_]的函数进行比较(图3.3.26)。计算曲线S(实线)与纵轴的截距是任意选取的,而斜率是理论预测的。
shell¿180 vs. 0中[C0§~]的观测斜率。暗实验中universa为-0.0022±0.0004%o (//mol kg-1)-1,而理论计算中S与[CO|_]在100 - 1000 //mol kg-1区间的平均斜率为-0.0024%o (//mol kg-1)-1。从这种巧合中可以得出以下结论:随着碳酸盐离子浓度的增加,O. universa中180的消耗可以用碳酸氢盐和碳酸盐的钙化摄取来解释(注意,这种描述被简化了——同位素分配的计算不是简单的质量平衡计算,见C.9节)。随着溶液中的组分从中等pW时的HCO3(同位素重)为主转变为高pH时的CO2-(同位素轻)为主,S的同位素组成减少,方解石的同位素组成也减少。结果表明,方解石明显是由碳酸氢盐和碳酸盐混合形成的,随着[CO2-]的增加,方解石(固体)和S(溶解)的氧同位素组成同样减少。
3.3.8 pH值对合成碳酸盐的影响
与前一节中描述的比较相似,将无机氧同位素分配(定量沉淀)的结果与Kim和O'Neil(1997)报道的从溶液中缓慢沉淀的合成碳酸盐(非定量沉淀)中的氧同位素效应进行了比较。然而,在这种情况下,对实验数据的分析并不像对O. universa的培养数据的分析那样直接。
Kim和O'Neil(1997)彻底研究了合成碳酸盐中的平衡氧同位素效应,并确定了氧的新值同位素分馏在低温下水和几种碳酸盐之间。令人惊讶的是,他们还发现同位素分馏在给定温度下,随着Ca2+/Ba2+和HCO3初始浓度的增加,水与碳酸盐(如方解石(CaC03)和毒白云石(BaC03)之间的关系增加(图3.3.27)。他们认为这些影响是非平衡分馏,因为应该只有一种平衡分馏在任何温度下。然而,这表明,观察到的影响是平衡分馏表示在不同的pW的溶液。
在接下来的讨论中考虑方解石,然而,所提出的结果应适用于碳酸盐一般将证明为毒钨石。Kim和O'Neil(1997)通过溶解来制备他们的溶液
40 35 30 25 20
15日10

图3.3.27:Kim和O'Neil(1997)测定的方解石与水之间氧同位素分馏随温度和不同初始Ca2+和HCO^~浓度的函数:5 mmol kg-1(实线),15 mmol kg-1(虚线),25 mmol kg-1(点虚线)。
去离子水中CaCl2和NaHC03的等摩尔浓度,浓度范围为5 ~ 25 mmol kg-1。通过向溶液中鼓泡氮气来去除二氧化碳,从而增加溶液的过饱和,从而促进了缓慢的沉淀。co2的去除伴随着pH值和[COl~]的增加,直到达到过饱和([COg -]c)的临界状态,碳酸钙开始析出(没有使用种子)。由于相应的临界pR是溶解无机碳总量的函数,因此过饱和的临界状态取决于HC03的初始浓度。这种效应可以用溶解的碳酸盐物种的浓度作为ph值的函数来说明,如图203页的图3.3.22所示。随着pH值的增加,HCO3转化为CO2,碳酸盐离子浓度增加,直到所有溶解的碳酸盐基本上都是碳酸盐离子。对于图3.3.22所示的溶液组成(HC02 = 2 mmol kg-1), pH值必须增加到约8,以达到过饱和的临界状态,例如[C02_]c = 10-2 mmol kg*-1。然而,如果EC02较小(对应于较低的初始浓度HCO.^), pll必须进一步增加以达到相同的过饱和临界状态。
正如Zeebe(1999)中详细描述的那样,Kim和O'Neil(1997)研究的溶液的临界pU值可以分别在Ca2+和HCO3初始浓度为5、15和25 mmol kg-1时估计为7.8、6.9和6.6。这些值是计算方解石沉淀,假设临界过饱和sc = 2。临界过饱和可以写成(Stumrn and Morgan, 1996):
其中7’为活度系数,[CO3-]为临界碳酸盐离子浓度,log A’= - 8.45为19°C时方解石在淡水中的溶解度积(Plummer and Busenberg, 1982)。
到目前为止所提出的考虑的基本结果如下。假设临界pH值代表方解石沉淀的平均pH值,并且在碳酸盐和水之间的每一个p\\氧同位素平衡都建立起来,那么根据第3.3.5节(参见图3.3.23,204页)提出的理论,S的同位素组成以及方解石的同位素组成随着临界pH值(或较低的初始浓度)而降低。
Kim和O'Neil(1997)给出的在19°C不同初始浓度下(钻石)方解石/毒白云石与水之间的氧同位素分馏值,以及在19°C和临界过饱和S = 2时根据临界pi I值计算的S与水之间的氧同位素分馏值(实线)如图3.3.28所示。为了在同一图中绘制方解石和毒重石的数值,在19°C和初始浓度为5 mmol kg-1时,将方解石与水、毒重石与水(~2.59%o)的平衡分馏差加到毒重石的数值中。强调了计算曲线S与纵轴的截距是任意选取的。由于实验的实际临界锁相环值是未知的,绝对值是无法比较的。通过在1 ~ 8之间改变过饱和sc来检验不同临界pH值对曲线形状的影响,而过饱和sc仅对曲线形状有边际影响。记住必要的假设
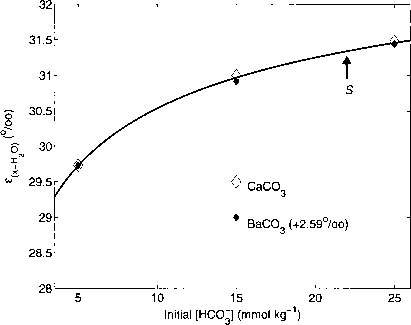
图3.3.28:Kim和O'Neil(1997)测定的水与方解石(裸露钻石)、水与毒白云石(填充钻石)之间的氧同位素分馏以及S(实线)在19°C时作为HCO^初始浓度的函数。计算曲线的截距任意选取;过饱和设定为sc = 2(见正文)。在毒钨矿的值上添加2.59%o的值。在这个表示中,方解石和毒锰石在初始浓度为5mmol kg-1时的值是相同的。
图3.3.28:Kim和O'Neil(1997)测定的水与方解石(裸露钻石)、水与毒白云石(填充钻石)之间的氧同位素分馏以及S(实线)在19°C时作为HCO^初始浓度的函数。计算曲线的截距任意选取;过饱和设定为sc = 2(见正文)。在毒钨矿的值上添加2.59%o的值。在这个表示中,方解石和毒锰石在初始浓度为5mmol kg-1时的值是相同的。
得到的理论推导分馏曲线与实验数据吻合良好。
虽然水与CaC03、水与BaC03的绝对分馏量有很大差异,但随着HCOg初始浓度的增加,分馏量的增加几乎是相同的。这一结果表明,所描述的效应是由溶液化学引起的,而不是由与晶体生长相关的不同的非平衡(动力学)分馏效应引起的。综上所述,Kim和O'Neil(1997)所描述的非平衡分馏可以用在单一温度和不同pH下的多次平衡分馏来解释。
本节只能列举几个在海洋科学中使用稳定氧同位素的例子。虽然还有许多其他的应用,但它们当然不能全部在本书中讨论。尽管如此,到目前为止的讨论已经展示了这个多种工具的强大功能。现在我们将转向讨论海洋环境中稳定的硼同位素。
3.4硼
近年来,硼同位素在化学海洋学中受到了广泛的关注,部分原因是它们被用作重建古ph值的一种手段。Spivack et al.(1993)利用浮游有孔虫的硼同位素组成重建了过去2000万年间表层海洋的pH值。Palmer et al.(1998)使用类似的方法重建了同一时间间隔内过去海洋的pll深度剖面。值得注意的是,根据硼同位素重建古ph值受限于硼在海水中的停留时间,约为1000万年至2000万年(参见218页方框)。在更长的时间尺度上,海洋中的硼同位素组成可能与今天不同,不能通过使用古代用物来估计——关于建模方法,见Lemarchand et al.(2000)。Sanyal等人(1995)利用稳定的硼同位素分析研究了地球历史上较近时期的气候变化。raybet雷竞技最新他们发现证据表明,在最后一次冰期(LGM, ~ 18.000年B.P.),冰川表面和深海的pH值较高。最近,珊瑚硼同位素组成的季节性变化被用来阐明珊瑚钙化过程和珊瑚¿13C记录(Hemming等人,1998b)。
本节简要总结了硼同位素在某些陆地化合物中的自然变化(回顾见Palmer和Swihart(1996))。然后讨论硼的同位素在硼的溶解物种之间的分配原理,以及硼在生物成因(如有孔虫!)和无机碳酸钙中的掺入。
3.4.1自然变异
图3.4.29显示了一些陆地化合物硼同位素组成的自然变化。与NBS SRM 951硼酸标准相比,海洋中总溶解硼(BT)的¿nB值为39.5%0
11111111来自大陆的碎屑 |
1 |
深海粘土 |
|
改变玄武岩 |
|
大洋中脊玄武岩 |
|
生物硅 |
|
海相碳酸盐岩ii |
海水 1 |
图3.4.29:一些陆地化合物的硼同位素组成(相对于NBS SRM 951硼酸标准)。
并且在整个世界海洋中是相当稳定的(Spivack和Edmond, 1987;Hemming和Hanson, 1992),因为硼在海洋中的停留时间很长(参见218页的方框)。海洋中硼的“重”硼同位素组成(相对于平均大陆地壳较重)似乎是一个谜,因为进入海洋的主要硼来自大陆的碎屑,其¿11B值约为- 15%至- 8% (Ishikawa和Nakamura, 1993)。前提是地球化学循环硼处于稳定状态时,必须从海洋中去除一定量的硼(等于每个时间间隔的硼输入量),其同位素组成与输入量相等。
因此,机制必须是活跃的,优先去除10B,从而相对于输入丰富了海洋中溶解的海水硼的硼同位素组成。硼在海洋中的三种主要下沉也改变了海水中硼的溶解:(1)硼在粘土上的吸附。(2)与海洋地壳交换;(3)与碳酸钙共沉淀(见施瓦茨等(1969);斯皮瓦克和埃德蒙(1987);Palmer et al. (1987);Vengosh等人(1991);Ishikawa和Nakamura(1993))。
Schwarcz等人(1969)和Palmer等人(1987)通过实验证明,吸附在海洋粘土上的硼相对于海水中溶解的硼在11B中被耗尽——分馏的大小是p\\相关的(见第3.4.2节)。Ishikawa和Nakamura(1993)测量了硼的浓度和^111!雷竞技csgo深海沉积物中粘土的值和报告的高浓度(96 - 132ppm),¿nB值介于- 6%o和+2.8%0之间(图3.4.29)。因此,粘土对硼的吸附是去除海洋中同位素轻硼的重要过程。
不变的(新)大洋中脊玄武岩(MORB)的¿11B值在- 2%0和-4%o之间。而蚀变玄武岩的IS值为^11,介于0%o和-|-10%o之间(Spivack和Edmond, 1987)。11年的丰富性!蚀变玄武岩可能是玄武岩与海水反应的结果。Spivack和Edmond(1987)估计,在他们的一些变质玄武岩样品中发现的硼95%以上可能来自海水。来自海水的玄武岩中次生硼的硼同位素组成比海水中的硼轻30%左右。因此,当一片海水与新鲜玄武岩发生反应时,水中的硼浓度会降低,而¿nB会增加。这一过程从海洋中去除了大量的硼,并增加了硼的同位素组成。
现代海洋生物碳酸盐(如有孔虫、翼足类、珊瑚)和现代深海碳酸盐沉积物的硼同位素组成约为+10%o至+30%o (Vengosh et al., 1991;亨明和汉森,1992年;Ishikawa和Nakamura, 1993)。11 B在海洋碳酸盐中相对于BT的同位素组成的消耗可能是由于B(OH)^优先吸收到在海水pH值下同位素比BT轻的碳酸盐中(见第3.4.3节)。据信,硼在海洋碳酸盐中的共沉淀占硼在海洋中总下沉量的20%左右(Vengosh et al., 1991)。
硼在海洋中的停留时间。在稳态状态下,某种元素在海洋中的停留时间r可以用该元素在海水中的总库存量除以每年的投入/产出的比值来估计,例如:Bt x M0
其中Bt = 4.52 ppm (= 4.52 × 10~6 g B / g海水)(Hemming and Hanson, 1992), Mo w 1.4 × 1024 g为海洋质量,Binput为以克/年为单位向海洋输入的硼。使用30 - 50 x 1010 g yr_1的硼输入(Vengosh et al., 1991),硼在海洋中的停留时间为1300 - 2100万年(Ma)。Lemarchand等人(2000年)的最新估计是14 Ma。
综上所述,相对于输入同位素组成,海洋中溶解的硼中11B的富集可以解释为与硼吸附到粘土、与海洋地壳交换以及与碳酸钙共沉淀等过程相关的优先去除10B。
生物硅(放射藻和硅藻)的硼同位素组成也有报道。它在2%0 ~ 5%之间,这与海水和二氧化硅中晶格键合硼的硼同位素平衡相一致(Ishikawa and Nakamura, 1993)。
新鲜玄武岩样品a的硼同位素组成为- 2%。计算样品A和海水之间的分馏,£(A - B)>(样品B,¿> B = 39.5%o)。还计算E(b_a),并将结果与6个值的差进行比较。
3.4.2硼同位素分配
硼有两种稳定的同位素(参考3.1.4节),10B和nB,分别占硼总量的19.82%和80.18% (IUPAC, 1998)。硼在海水中的主要溶解种类是B(OH)3和B(OH)^~,它们之间通过化学平衡连接:
B(oh)3 + h20 ^ B(oh)"+ h + (3.4.42)
这些物种的典型海水浓度作为pR的函数显示在图3.4.30a中。在低pH值下所有溶解的硼基本上是硼酸,B(OH)3,而在高pH值下所有溶解的硼基本上是硼酸离子,B(OH)^ 9其中[B(OH)3] =硼酸的pK*值
9多核硼类如B303(0H)^~, B^s^H)2-和B506(0H)7在浓度小于25 mmol kg-1时可以忽略不计(Su和Suarez, 1995),在典型海水浓度为~0.4 mmol kg-1时可以忽略不计。
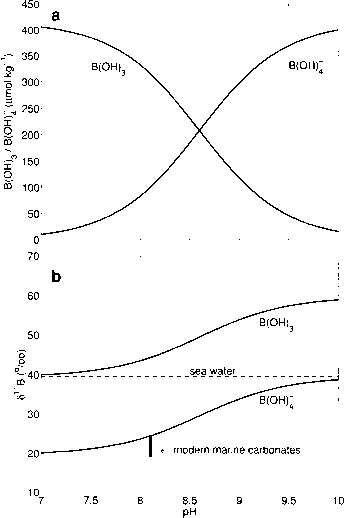
图3.4.30:(a.)溶解态硼的浓度与pH值的函数关系(T = 25°C, S = 35)。硼酸pKg的解离常数为8.60;总硼浓度为416 //mol kg“”1 (DOE, 1994)。(b) b (OH),3和b (OH)^~的硼同位素组成作为pR的函数(cf. Hemming and Hanson(1992))。
图3.4.30:(a.)溶解态硼的浓度与pH值的函数关系(T = 25°C, S = 35)。硼酸pKg的解离常数为8.60;总硼浓度为416 //mol kg“”1 (DOE, 1994)。(b) b (OH),3和b (OH)^~的硼同位素组成作为pR的函数(cf. Hemming and Hanson(1992))。
[B(OII)7]为8.60,T = 25°C, S = 35 (DOE, 1994)。在离子强度I = 0.68的NaCl溶液中,pKB在25°C下的硼酸解离常数值为8.830 (Hershey et al., 1986)也用于海水(海水离子强度是0.697)。Hershey等人(1986)还测定了Na-Ca-Cl和Na-Mg-Cl溶液在T = 25°C (I = 0.68)下的pKg分别为8.675和8.725,接近海水值8.60 (DOE, 1994),表明Ca2+和Mg2+离子对pK*:s的影响(~0.1单位)。因此,在计算海洋中溶解的硼的浓度时,使用在海水中测定的pA'g可能更为准确。
利用海水总硼浓度
Bt = [B(OH)3] + [B(OH)4-] (3.4.43)
当BT = 416.0 x(5/35) /¿mol kg"1 (DOE, 1994)时,可以计算出溶解物种的浓度。用硼酸的解离常数:
Ab - [B(OH)3] ' (3A44)
B(OH)3和B(OH)4在任意pH下的浓度为:
[B(0H»f = iTWm <3A-46'
与B(OH)4相比,稳定同位素nB在B(OH)3中富集,因此溶解组分的同位素组成随pH值的变化而变化(图3.4.30b)。在低pM时,B(OH)3的同位素组成等于总溶解硼的同位素组成~39.5%o。相反,在高pH时,B(OH)4的同位素组成等于总溶解硼的同位素组成。在这两者之间,两种物质的<5nB都发生了变化,B(OH)3相对于B(OH)4在任何ph下都在平衡状态下富集了约20%o (Kakihana et al., 1977)。B(OH)3和B(OH)4之间的硼同位素分配作为pli的函数如图3.4.30b所示。
图3.4.30b所示的同位素划分可计算如下:总溶解硼的6nB由质量平衡关系10给出:
^UB(bt) x bt = S^B{Bmh) x [B(OH)3]
+¿llB(B(OH)-) x [B(°H)4-] (3-4.47)
10在质量平衡方程(参见第3.1.5节)中,用8个值代替丰度分数(r = r /(1 + r))引入的溶解硼种类的8个值的误差小于0.08%o。
b (0H)3与b (OH)4的分馏因子£b由
- B = fli^l-AxlO3 \W(B(OH)-) /
其中ay = 1.0194在25°C (Kakihana et al., 1977)。利用两种物质1和2的同位素比值与6个值之间的关系:
我们有:
éllB(B(OH)3, = éilB(B(OH)r)«B + ^B (3.4.49)
将式(3.4.49)代入式(3.4.47),求解^ B(B(0H)~)为:
^BBrBT-,B[B(OH)3],, 4 r>())
(B(OH)~) - [B(OH)4-] + aB[B(OH)3] ' ('3'4"JU)
由于au非常接近单位,它可以近似为:
1, H (B (OH) -, = * 11,该剧ib (B (OH) 3) / Bt,和我“B (g |哦),|可以写成:
éllR(B(OH)3) = *11b(B(OH)4-) +"B '
因此,给定硼的总浓度By、By的同位素组成和分馏因子cb,可以在任意/jH下计算B(OH)3和8(011)^的同位素组成。
Kakihana等人(1977)给出的溶解硼物种间同位素分配的分馏因子oB = 1.0194(25°C)表明对温度的依赖性较弱(表3.4.10)(Kakihana和Kotaka, 1977;Kotaka and Kakihana, 1977)。它是根据同位素物质的热力学性质(Urey, 1947)计算出来的,这在第3.5节中详细讨论。据我们所知,还没有确定实验价值。因此理论推导值在文献中被广泛应用。
需要强调的是,在溶解的B(OH)3和B(OH)^之间的硼同位素分馏中,不应使用已采用的aB值1.032(取自Palmer et al.(1987)关于硼在海洋粘土上吸附的论文)。Palmer et al.(1987)测定了在pR值从6.5到8.5范围内,海水中溶解的硼和吸附在海洋粘土上的硼之间的硼分布系数和同位素分馏。Palmer et al.(1987)给出的分馏因子0.969和0.992(分别相当于1.032和1.008)11,是指溶液中溶解的硼与粘土上吸附的硼之间的同位素分馏因子。即,B(OH)3在溶液中与各吸附组分之间的分馏为- 32%0,而B(OH)4在溶液中与各吸附组分之间的分馏为- 8%0。因此1.0320的值不是溶解的B(OH)3和B(OH)4之间的分馏因子ctg。然而,人们可以根据Palmer等人的数据估计aB(参见本节末尾的注释)。
上面讨论的例子指出,如果没有实验值,从第一原理(参见Richet et al., 1977)确定分馏因子的理论方法是有用的。对于计算分馏因子至关重要的是所考虑的分子的振动频率。
Tc(°C) |
a (B (OH) 3 B (OH) 4”) |
0 |
1.0206 |
5 |
1.0204 |
15 |
1.0199 |
25 |
1.0194 |
40 |
1.0187 |
50 |
1.0181 |
60 |
1.0177 |
为了简化硼同位素在溶解态硼物种间的分配计算,Kakihana和Kotaka(1977)采用了近似的方法
这里使用11个大于1的分馏因子,即1.0320 = 0.969-1来比较Palmer等人(1987)的值(他们认为i?(吸附)/i?(溶液)小于1)与Kakihana等人(1977)的计算值(他们认为#(B(OH)3)/. k (B(OH)-)大于1,cf. Eq.(3.4.48))。
由7个原子组成的三角形平面B(OH)3分子(图3.4.34,231页)与仅由4个原子组成的分子相匹配,即他们将每个OH基近似为单个质量点。对于四面体分子B(OH)^,也采用了类似的方法。目前尚不清楚这些近似是否以及在何种程度上影响计算的硼同位素分馏因子。由于溶解的硼物种之间的分馏因子几乎进入了与水溶液中硼同位素分配相关的每一个计算,未来的工作应该通过实验确定分馏因子,或者应该改进Kak-ihana和Kotaka(1977)的计算。
备注:
基于几个假设,可以从Palmer等人(1987)的发现中得出ftg的值如下。假设B(0H)4是吸附在粘土上的唯一组分,随着B(0H)4在溶液中的比例从0增加到40%,吸附硼的量增加了2倍,从而支持了B(0H)4在粘土上的吸附。进一步假设溶解的BfOHlJ与吸附的硼之间存在恒定的分馏,则吸附硼的同位素组成将遵循B(OH)4”的inB与pH值的曲线(参见图3.4.30),其偏移量恒定为-8%o (Palmer et al.(1987)给出的B(OH)4与吸附硼之间的分馏为-8%o)。因此,在非常高的pH值下,吸附的硼比总溶解硼的¿nB轻约8%(所有溶解的硼基本上都是BiOH)^),而在非常低的pH值下,吸附的硼比6n ByT轻8%,再加上等于B(OH)3和B(OH)4 (an)之间的分馏量。根据Palmer et al.(1987)给出的B(OH)3(在很低pH值时= Bj)与吸附硼之间的分馏为-32%o, ag为~24%o。综上所述,用这种方法得到的t»e等于Palmer et al.给出的分式因子的差值,即约为,24%,o,这与Kakihana et al.(1977)计算的~20%o的分式相似(考虑到Palmer et al.插值的误差)。
在自然界中,“轻”稳定同位素12C和leO分别比“重”同位素1,1c和J,0更丰富,而硼则相反(UB比10B更丰富)。考虑到这些稳定同位素的原子核中质子和中子的数量(参见第3.1节),硼有什么不同?
考虑图3.4.30a。假设硼酸的pK*值为9.0。B(OH)~和B(OH)3的曲线是怎样的?B(OH)~ at, pH值8.2的¿nB值会比pA'g = 8.6计算的值更重还是更轻(图3.4.30b)。
表明在质量平衡方程(3.4.47)中,用b值代替分数丰度(r = r /(f + r))引入的溶解硼种b值的误差小于0.08%o(推导rg(oH)- ^^ rB(oH) 3>的方程,从这些方程中计算8个值,并将结果与用等式计算的8个值进行比较。(3.4.49)及(3.4.50))。
3.4.3碳酸钙中的硼
在从水溶液中析出CaC03的过程中,硼掺入方解石或文石晶格中。与晶体中碳的浓度相比,晶体中硼的浓度很小(在百万分之一的数量级)。Hemming和Hanson(1992)测量的现代海洋碳酸盐中硼的浓度在10.9到75.1 ppm之间变化很大相比之下,这些碳酸盐的硼同位素组成变化很小(图3.4.30b)。
假设方解石上只吸附了带电物质,则方解石的硼同位素组成随pH增加,类似于¿nB of B(OH)4随pH增加。最近在不同pK条件下的无机方解石沉淀实验证实了这一假设(Sanyal等人,2000年)(图3.4.31)。人工海水中析出的无机方解石溶解硼浓度比海水高17倍。由于种子用于沉淀,其中过度生长必须进行分析,高硼浓度是必要的,以产生足够的硼质谱。Sanyal等人(2000)研究了三种不同pW值(7.9、8.3和8.6)下的硼同位素分馏,并观察到¿nB随着pU的增加而明显增加——无机方解石<*>nB对pH值的斜率与溶解物种B(OH)4对pE的6nB斜率的计算结果一致(图3.4.31)13。然而,值得注意的是,如果理论计算的B(OH)4和B(0H)3之间的分馏是正确的(Kakihana et al., 1977),则无机方解石的硼同位素组成比B(OH)4轻约5%。
这里单位ppm指的是重量的百万分之数。例如,现代海水中硼的总浓度为4.52 ppm,可以表示为4.52 x10 "6千克B /千克海水= 4.52毫克kg-1。因为硼的相对原子量是10.811,所以它的相对原子量是418 /^mol kg-。
Sanyal等人(2000)使用总溶解硼(Bt)为6nB +l%o的人工海水获得¿nB值,并将811 Bns = 1.03846 x£nBAs + 38.46转换为天然海水规模(inBBT = 39.5%o),其中1.03846是表示人工海水和天然海水之间差异的分馏因子:aNS_AS =(£ns + 103)/((5as + 103) =(39.5 + 103)/(1 + 103) = 1.03846。最后,811b值- 19.2、- 16.8和- 13.8%o(人工海水)在pH值7.9、8.3和8.6时,得到18.5、21.0和24.1%o(天然海水,参见图3.4.31)
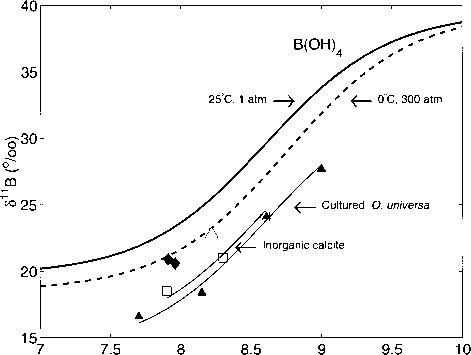
图3.4.31:B(OH)7在25℃时,P = 1 atm(实线,ftB = 1.0194, pK£= 8.60)和0℃时,P = 300 atm(虚线,aB = 1.0206, pAy = 8.75)的硼同位素组成。还显示了无机方解石(正方形)、人工培养的浮游有孔虫(Orbulina universa,填充三角形)、全新世浮游有孔虫(Globigtrinoidvs sacculifer,开放三角形)和全新世混合底栖有孔虫(菱形)的¿× "B值。数据来自Sanyal等人(1995;1996;2000)。
图3.4.31:B(OH)7在25℃时,P = 1 atm(实线,ftB = 1.0194, pK£= 8.60)和0℃时,P = 300 atm(虚线,aB = 1.0206, pAy = 8.75)的硼同位素组成。还显示了无机方解石(正方形)、人工培养的浮游有孔虫(Orbulina universa,填充三角形)、全新世浮游有孔虫(Globigtrinoidvs sacculifer,开放三角形)和全新世混合底栖有孔虫(菱形)的¿× "B值。数据来自Sanyal等人(1995;1996;2000)。
在不同pH值培养的浮游有孔虫Orbulina universa(图3.4.31)的生物方解石中也观察到类似的行为(Sanyal et al..1996)。在这种情况下,¿nB也遵循计算线的斜率,但方解石比li(011)轻约6%。似乎Orbulina universa的硼同位素组成比浮游有孔虫Globigerinoides sacculifer的硼同位素组成要轻(图3.4.31中的开三角形;来自大西洋和太平洋全新世沉积物岩芯样品的数据,Sanyal等,1995)。这个特性不太可能是文化实验的产物,因为生活在0。来自南加州湾的universa和沉积物芯顶样品的贝壳的¿nB值与培养的0。在相同的pH值(~ 8.15)下。最重要的是,最近对小球藻的培养实验结果表明,<5nB的小球藻对周围海水pH值变化的响应与0。universa - G. sacculifer中的¿nB值确实始终比0. sacculifer中的值重。 universa (A. Sanyal, J. Bijma, pers. comm.). The most simple explanation of the difference between 0. universa and G. sacculifer is a vital effect, possibly adding a constant (negative) offset at any pH to the isotopic signal of B(0H)4 which is thought to be adsorbed on the calcite (Sanyal et al., 1996).
总之,生物(和无机)CaC03的<511B与形成它的溶液的pH值有明显的趋势——这一趋势与理论预测的B(0H)4¿11B与pH值的斜率相一致(图3.4.31)。因此,有孔虫方解石的硼同位素组成可以用作古ph记录器(例如Sanyal等人,1995年;Palmer et al., 1998)。这一说法最近得到了证实,证明与硼掺入生物源CaC03相关的动力学效应不太可能(Zeebe et al., 2001)。然而,值得注意的是,为了利用稳定硼同位素的潜力,其他关键参数,如硼在海洋中的停留时间(Lemarchand et al., 2000)和重要影响也必须仔细评估。
碳酸盐形成时的海水pH值可由碳酸盐的硼同位素组成计算如下。基于碳酸盐岩的同位素组成¿n Bc等于带电物种的同位素组成14的假设,<^11B(b(oh)-)'等式。(3.4.44)和(3.4.45)可用于求解[11+]的式(3.4.50):pH = -log([H+])
' B£BBt - aB£Bc -£g / ^
式中,piiB为硼酸的pK*值(pA’b在T = 25℃时= 8.60,
S = 35 (DOE, 1994)), <*>x1BBt = 39.5%o为现代海水硼同位素组成,aB = 1.0194为B(OH)4之间的分馏因子
和B(OH)3在25°C (Kakihana等,1977),和= (aB - 1) X 103。
例如,如果测量碳酸盐的硼同位素组成,
¿11Bc,是24%0,我们有:
N™1 (39'5 - 24
否则,碳酸盐的同位素组成可能会增加一个恒定的偏移量。
计算的pll值取决于011 pA'B,在文献中使用了不同的值(参见第3.4.2节)。避免这种并发症的一种方法是研究海水pH值的变化,而不是绝对值(例如Sanyal等人。1995)。pH值估计值也受分馏因子aB的影响(见第3.4.2节的讨论)。例如,qb变化0.001 (sB变化l%o)导致式(3.4.52)中估计pH值的变化约为0.1个pH单位。
末次冰期沉积物岩心中硼同位素组成为~25%o,而现代球花的硼同位素组成为23%o左右。关于冰川表层海洋的pH值,你能得出什么结论?
假设表层海洋pH值确实随硼同位素的变化而变化,如果SJCO2与今天大致相同,碳酸盐离子浓度会发生什么变化?这与在冰芯中观察到的冰川大气中较低的二氧化碳浓度是否一致?
3.4.4碳酸钙中硼的丰度
Hemming和Hanson(1992)观察到的海洋碳酸盐的同位素组成似乎与硼丰度相关(图3.4.32)。/>llB值随碳酸盐中硼丰度的增加而增大。在有孔虫的壳中也观察到类似的行为(Sanyal et al..1996年)和无机方解石(Sanyal等。2000),硼浓度与¿nB之间有很强的相关性(图3.4.32)。这种行为与B(OH)J吸附在碳酸盐表面的模型是一致的。随着pH值的增加,B(OH)4的浓度和其同位素组成增加(图3.4.30)。带电荷的B(OH>4)更容易被吸引到晶体表面——溶液中B(OH)J浓度的增加(在更高的pH值下)将导致碳酸盐中硼的丰度增加。同时,B(OH)J的硼同位素组成增加,从而导致碳酸盐的泰国。该模型与在各种碳酸盐中观察到的硼丰度和硼同位素组成之间的关系是一致的(图3.4.32)。 The relationship is, however, different for example for calcite and aragonite - this subject is discussed below.
Hemming和Hanson(1992)提出了碳酸盐中CO^-位硼取代的机理如下:
28 r
培养的O. universa
“lO 20 18 16
无机方解石
图3.4.32”。碳酸盐岩中硼同位素组成及硼丰度。填充圈:海洋高镁方解石和方解石,开放圈:海洋文石(Hemming and Hanson, 1992)。正方形:无机方解石(三亚.1等,2000)。三角形:有孔方解石(Sanyal et al., 1996)。随着pH(和[B(OH)^~])的增加,碳酸盐的inB和硼丰度增加。这种行为与B(OH)^~吸附在碳酸盐表面是一致的。
图3.4.32”。碳酸盐岩中硼同位素组成及硼丰度。填充圈:海洋高镁方解石和方解石,开放圈:海洋文石(Hemming and Hanson, 1992)。正方形:无机方解石(三亚.1等,2000)。三角形:有孔方解石(Sanyal et al., 1996)。随着pH(和[B(OH)^~])的增加,碳酸盐的inB和硼丰度增加。这种行为与B(OH)^~吸附在碳酸盐表面是一致的。
CaC03 + B(OH)"-)•Ca(HB03) + HCOJ + H20 (3.4.53)
Kd = ^rzx-z^r* - (3-4-54)
碳酸盐中硼取代的交换分配系数KD可表示为:
[HBOg-ZCOg-Ud [B (0 h) 4 - / HC03]液体
描述固体中硼碳比与硼酸-二碳比的比值。流体中氢酸盐的比例。这里重要的是,液体中的比例指的是硼酸离子浓度,而不是溶解的硼总量。硼分布系数可由Hemming and Hanson(1992)的数据(表3.4.11)计算如下:
[B(ppm)] x lO"6 x MCaC0JMB
其中。l/(a(-() = 100 g, MB = 10.8 g分别为CaC03和B的摩尔质量。利用硼同位素组成和式(3.4.51),可以估算出pH值和B(OH)7的浓度。Hemming和Hanson(1992)发现,他们的数据可以通过假设HCO3浓度为142 ppm (2330 //mol kg-1)来最好地近似,这样KD的平均值为0.012。
(%) |
(ppm) |
B(011)7 (//mol kg"1) |
HCO3 (//mol kg-1) |
Kn |
22.10 |
24.4 |
51 |
2330 |
0.010 |
22.90 |
36.7 |
68 |
2330 |
0.012 |
24.60 |
53.5 |
104 |
2330 |
0.011 |
aB(OH)”是用方程式从¿nBCaCo3中估计出来的。(3.4.46)及(3.4.51)。
aB(OH)”是用方程式从¿nBCaCo3中估计出来的。(3.4.46)及(3.4.51)。
表3.4.11列出了Hemming和Hanson(1992)给出的三个数据示例,而完整的数据集如图3.4.33所示。还显示了无机方解石和有孔虫方解石的结果,其中硼的分配系数KD是由与数据的线性拟合的斜率确定的无机和有孔孔方解石(KD分别为0.001和0.0001)的h d明显小于文石和高镁方解石(K{) = 0.012,参见Hemming et al., 1995)。这种现象可以解释为硼在文石和方解石中的配位不同(见3.4.5节)。值得注意的是,与浮游有孔虫Orbulina vniversn数据的线性拟合不与垂直轴相交于零,这表明即使溶液中的B(OH)J趋于零,方解石中硼的浓度也不会趋于零。如果B(OH)^是唯一吸附在方解石上的物质,那么它应该被吸附在方解石上。考虑到有孔虫,因此,模型(式(3.4.53))在碳酸盐中硼浓度低和溶液中B(OH)J浓度低时可能不能充分工作。然而,在所研究的所有碳酸盐中,固体中的硼碳比与流体中硼酸盐与碳酸氢盐的比例之间存在明显的相关性(图3.1.33)。这表明该模型总体上做得很好。
假设SCO2 = 2200 /(mol kg 1,
[B (0 h); / HC03 -] f | uic
0.25
3流体
图3.4.33:硼在碳酸盐中的分布系数I\d。填充圈:海洋高镁方解石和方解石,开放圈:海洋文石(Hemming and Hanson, 1992)。方格:人工海水中沉淀的无机方解石(Sanyal et al., 2000)。三角形:有孔虫方解石,从Orbulina universa培养实验(Sanyal et al., 1996)。为了将无机方解石的数据绘制到同一图表中,将无机方解石和人工海水(流体)的硼浓度除以17(这并不影响K'd的值,参见式(3.4.54))。
3.4.5硼配位
硼在方解石中主要呈三角形配位,而在文石中则呈四面体配位(Hemming等,1998a)。正如上一节所讨论的,碳酸钙的硼同位素分析显示,带电物种(B(OH)4)很可能是在降水过程中被吸收的,这一点在<5nB的各种海洋碳酸盐中很明显。
硼的溶解形式,B(OH)3和B(OH)4,分别表现为平面三角配位和四面体配位(图3.4.34)。因此,硼加入方解石晶格需要从吸附物种(B(OH)4)的四面体结构转变为方解石晶格中的(最终)三角配位。硼在文石中呈四面体配位,与文石结合不需要这种转变。这可能解释了相对于有孔虫方解石,海洋文石中硼的分布系数更高(图3.4.33)。Hemming等人(1995)在合成文石、高镁方解石和方解石(根据其相对硼丰度列出)中也观察到了同样的行为。
在pH值8.2时,物种%
这篇文章有用吗?